RAČUNOVODSTVO PAVLIHA

ČASOVNA VREDNOST DENARJA

ČASOVNA VREDNOST DENARJA

Ekonomski subjekt zahteva določeno nadomestilo zato, da se danes odreče uporabi razpoložljivega denarja. In čim daljši je čas, za katerega se odreče uporabi denarja, večje je nadomestilo. To nadomestilo pa imenujemo donos.

Torej ima enaka denarna enota za ekonomske subjekte različno vrednost glede na to, kdaj v času se porabi. Cilj poslovanja podjetja je maksimiziranje tržne vrednosti, ki je tem večja, če lastnikom prinese več denarja. Ni pa pomembna samo količina denarja, ampak tudi časovna razporeditev denarja.

NA VRH

PRIHODNJA VREDNOST

SPLOŠNO

Prihodnja vrednost označuje vsoto denarja, na katero bo narasla naložba v določenem časovnem obdobju. Če je to časovno obdobje daljše od časovnega obdobja, za katerega se obračunavajo obresti, se pri izračunu uporablja obrestno obrestni račun.

ENO PLAČILO

Če želimo izračunat koliko bo vredna vloga v banki v enem letu, če se obresti pripišejo po enem letu uporabimo formulo :

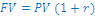
FV - future value oz. prihodnja vrednost
PV - glavnica
r - obrestna mera

Banka običajno pripisuje obresti ob koncu leta, oz. ob koncu določenega obdobja, ki je lahko tudi pol leta. Torej če imamo glavnico npr. 1000€ in obrestno mero 10%, bo prihodnja vrednost ob koncu leta 1100€. V drugem letu se obrestuje znesek 1100€ in prihodnja vrednost ob koncu drugega leta je 1.210€. Formula za ta izračun pa je naslednja :

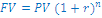
FV - prihodnja vrednost
r - obrestna mera
n - število obdobij obrestovanja
(1+r)ⁿ - faktor prihodnje vrednosti

Primer 1, Primer 2, Primer 6, Primer 7, Primer 8, Primer 9, Primer 10, Primer 13, Primer 14, Primer 15,

VEČKRATNA PLAČILA

V praksi pa se v glavnem dogaja, da imamo več različnih vplačil v različnih časovnih obdobjih. V takem primeru pa moramo za vsako vplačilo posebaj izračunati kakšna bo prihodnja vrednost. Splošna enačba prihodnje vrednosti za večkratna vplačila je naslednja :

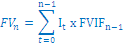
Pri čemer je FVIF = (1+r)ⁿ , torej faktor prihodnje vrednosti
n - število obdobij obrestovanja
I_t - glavnica obdobja t

Primer 3, Primer 11,

NA VRH

SEDANJA VREDNOST

SPLOŠNO

Sedanja vrednost je ravno nasprotni pojem od prihodnje vrednosti. Gre za to, da izračunamo koliko je nek prihodnji donos vreden danes. Če imamo npr. možnost vlagati prihranke v nekaj različnih naložb za katere vemo da nam bo prva npr. prinesla drugo leto 130€, druga čez leto in pol 150€, nas zanima, koliko pa sta ta dva donosa vredna danes.

ENO PLAČILO

Enačba za eno plačilo je naslednja :

PV - sedanja vrednost
FV - Prihodnja vrednost
r - diskontna stopnja
n - stevilo obdobij

Primer 4

VEČKRATNA PLAČILA

Če pa imamo opravka z več plačili ki jih bomo dobili v prihodnosti, pa uporabimo naslednjo enačbo

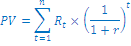
R - plačila
r - diskontna stopnja
n - število obdobij

NA VRH

Primer 5, Primer 12

formulex formule